Mathematics How to Read Large Theta and Small Theta
The Math Behind "Big O" and Other Asymptotic Notations
The formal definitions of notations like "Big O", "Big Omega", and "Large Theta".
![]()

Big O (pronounced "big oh") is a mathematical notation widely used in computer science to draw the efficiency of algorithms, either in terms of computational time or of retention space. The main purpose of this and other so-called asymptotic notations is to describe the behavior of mathematical functions, past comparing their "orders of growth".
In this article, I beginning give a quick overview of how the Big O notation is used in exercise to describe the efficiency of algorithms. Later on, I present its mathematical definition, as well equally those of other similar notations similar "Big Omega" (Ω) and "Large Theta" (Θ). Additionally, I also provide a couple of formal methods y'all tin utilise to classify mathematical functions co-ordinate to those definitions.
"Large O" in a Nutshell
Annotation: If you are used to working with algorithms, chances are y'all've used or seen the Big O notation before. If you believe that you lot already have a general understanding of what Big O means and how it is used to describe the efficiency of an algorithm, you lot tin can probably skip to the next section, where you lot'll find the mathematical definitions for Large O and other similar notations.
The Big O note is commonly used to distribute algorithms into a few Basic Efficiency Classes, like O(log(due north)), O(n), O(northward*log(north)), O(n²), and so on. Nosotros say that a standard linear search algorithm runs in O(n) because its running fourth dimension is expected to increase linearly with its input size. Similarly, we know that binary searches are O(log(n)), and the most efficient sorting algorithms tin can run in O(due north*log(n)).
Even so, saying that an algorithm is O(north²) doesn't mean that it performs exactly n² operations for a given input of size northward. Imagine that Algorithm A always performs f(due north)=2n²+n+one operations. What people ordinarily exercise with this office is to drop its non-ascendant terms (similar +n and +1) and its constants (like the 2 in 2n²) to obtain its asymptotic notation O(n²). If there is an Algorithm B that always performs f(north)=4n²+3n+3 operations, information technology tin can also exist described as O(n²), although information technology performs more than than twice the operations as Algorithm A for any value of due north.
Only there'due south nothing incorrect with that. When we utilize an asymptotic notation like Big O, we are interested in comparing orders of growth, instead of caring near verbal numbers. The master goal of this analysis is to describe how the running time or memory-space required by an algorithm increases depending on the input size n, especially when n is considerably large.
If an algorithm is O(n²), that means that if nosotros double the input size, then the number of operations performed will be roughly quadrupled. By increasing n=100 to n=200, the number of operations performed by Algorithm A will go from 20,101 to lxxx,201 operations, while for Algorithm B this number will go from twoscore,303 to 160,603 operations. The number of operations performed by each algorithm gets multiplied by roughly four (although non exactly).
On the other hand, algorithms that are O(2ⁿ) or O(n!) have much higher orders of growth, and that tin can exist noticed fifty-fifty for small values of n. For instance, just going from n=x to n=twenty will crusade an O(2ⁿ) algorithm to perform roughly 1024 more operations. And, for an O(n!) algorithm, that would hateful more than than 670 billion times more operations equally before.
Formal Definitions of Asymptotic Notations
If you weren't so familiar with the Large O note, I hope that the quick introduction to a higher place was plenty to give y'all a general understanding of how an asymptotic notation like Big O works, and why it makes then much sense to apply this ceremonial when evaluating the efficiency of algorithms. If yous feel similar you still don't fully empathize this concept, maybe yous should check other manufactures with additional examples (like this ane) before getting into the more complex mathematical definitions that will be discussed in this article.
In the following, I will get deeper into how Big O is mathematically divers. I will as well introduce a few other like asymptotic notations that are also used in information science to evaluate the efficiency of algorithms.
Big O: Upper Bounds
And then far, I've been using the Big O notation the style it's most commonly used: as an exact description of an algorithm'south efficiency. However, that is non technically correct — equally I will show below, Big O simply provides a mode to represent upper bounds. So keep in heed that from at present on I will offset referring to Big O according to how it'southward mathematically defined, instead of how information technology's normally used in practice. (If you lot are interested in a deeper discussion most this very mutual misconception, you can bank check this previous article of mine.)
Informally, O(g(n)) can be understood every bit the fix of mathematical functions that contains all functions that don't "grow faster" than g(n). For instance, O(n²) is the fix that contains n²+3n, 3n, northward, log(n), and infinite other functions that practice non grow faster than f(north)=n² when due north → ∞.
At present, hither's how Large O is formally divers:
f(n)∈ O(thou(n)) if and simply if there exist some positive constant c and some nonnegative integer nₒ such that f(north) ≤ cg(n) for all due north ≥ nₒ.
For instance, let's check if 3n∈ O(n²). Taking c=ane and plotting the functions f(n)=3n and cg(n)=1n², we tin see that both intersect at nₒ=3:
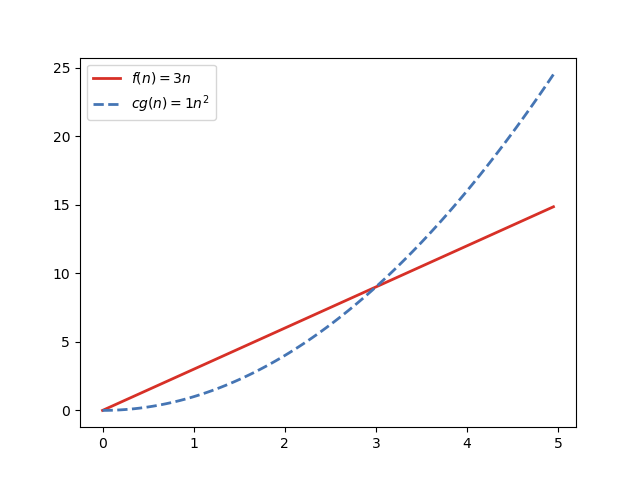
Looking at the plot, nosotros tin easily tell that 3n ≤ 1n² for all n≥3. But that'due south not enough, as we need to actually prove that. We tin can employ mathematical induction to do information technology. It goes like this:
- Nosotros need a base case nₒ for which we know that f(nₒ) ≤ cg(nₒ). Merely we already have 1, as we know that we tin use nₒ=3.
- Then nosotros assume that f(due north)≤cg(n) for a given due north≥nₒ. In our case, nosotros assume that 3n ≤ 1n² for a given due north≥3.
- Now we need to evidence that if f(northward)≤cg(n), so f(n+1) ≤ cg(n+1). In our case, we need to evidence that if our assumption (2) above is true, then 3(n+ane) ≤ (n+1)² is also true. This can likewise be written equally 3n+3 ≤ n² + 2n + 1. But, since we already know from (2) that 3n ≤ n², we can subtract 3n from the left side and north² from the correct side of the inequality, without affecting its relation. This will requite us 3 ≤ 2n+i. Equally we know that north≥3, this inequality will always be true provided that (ii) holds true. This completes the proof that 3n ≤ 1n² for all northward≥3, and therefore 3n ∈ O(n²).
Note: In that location'south a much more convenient mode to bank check if f(n)∈ O(g(n)) for two given functions f(northward) and m(north). This will be discussed further in this commodity, after nosotros're done presenting the formal definitions of some other asymptotic functions.
Big Omega (Ω): Lower bounds
Big Omega is defined in a similar way as Big O, except that it represents a lower bound instead of an upper bound. Thus, its formal definition only reverses the relation between f(n) and cg(due north). In other words, "≤" becomes "≥":
f(n)∈ Ω(g(north)) if and simply if at that place exist some positive constant c and some nonnegative integer nₒ such that f(north)≥cg(northward) for all northward ≥ nₒ.
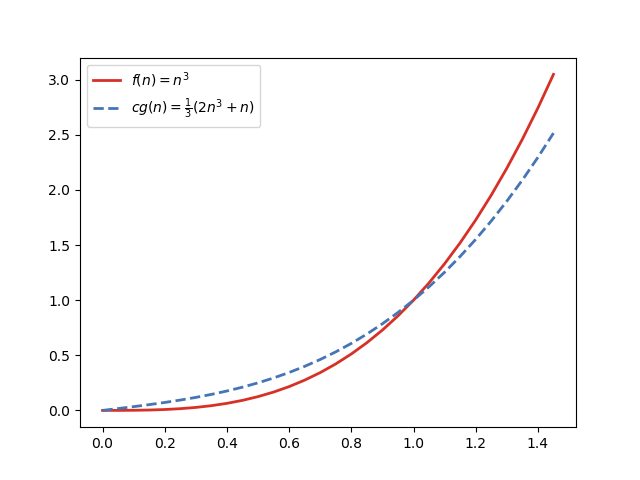
As an example, consider that n³∈ Ω(2n³+north). To prove this statement, yous may effort c=ane/iii and n=1, and use the consecration arroyo equally described in a higher place. Here'south a graphical representation:
Big Theta (Θ): Tight bounds
Chip Theta is used to represent tight bounds for functions. Saying that f(n)∈ Θ(g(due north)) means that f(n) has exactly the same order of growth as chiliad(n).
Basically, Big Theta is the intersection of Big O and Large Omega. Here are ii simple definitions for Large Theta based on that fact:
one) f(n) ∈ Θ(chiliad(n)) if and only if f(n) ∈ O(yard(northward)) and f(n) ∈ Ω(g(n)).
ii) Θ(m(n))=O(g(due north)) ⋂ Ω(g(n)).
Simply Large Theta tin also be defined similarly as how nosotros've defined Large O and Large Omega above, by merging both definitions together:
f(n)∈ Θ(yard(n)) if and simply if there exist some positive constants c₁ and c₂ and some nonnegative integer nₒ such that c₁ g(n) ≤ f(n) ≤ c₂ g(northward) for all northward ≥ nₒ.
Merely like we did for Big Omega, we can also evidence that n³∈ Θ(2n³+due north). For that, consider c₁=1/iii, c₂=1/two, and nₒ=ane:

Fiddling Omega (ω) and Fiddling O (o): Loose bounds
That is right, asymptotic notations are not always Large. There are also these ii Little notations: Little Omega (ω) and Lilliputian O (o). They are not used as much as the Large ones, simply I similar to mention them for the sake of abyss.
These two notations are used to represent lower or upper premises that are non "tight". More specifically, ω(1000(n)) includes all functions that are in Ω(g(n)) but non in Θ(g(n)). Formally, ω(g(n)) = Ω(g(northward)) – Θ(g(n)). Likewise, o(g(n)) = O(g(north)) – Θ(chiliad(northward)).
For instance, due north²∈ o(due north³), but due north³∉ o(n³).
Here are the formal definitions for these two Little notations:
f(n)∈ o(k(n)) if and just if in that location exists a nonnegative integer nₒ such that f(north)≤cg(n) for all n ≥ nₒ and for any positive abiding c.
f(northward)∈ ω(g(n)) if and but if there exists a nonnegative integer nₒ such that f(n)≥cg(n) for all north ≥ nₒ and for any positive constant c.
Did you get the divergence? While for Big Omega and Large O a single value of c is enough, Petty Omega and Trivial O crave the holding to be valid for any value of c.
Using Limits To Compare Two Functions
In the examples above I've shown how you lot can apply mathematical induction to evidence whether f(n)∈ O(thousand(n)), for whatsoever two arbitrary functions f(n) and one thousand(n). But there's a much more handy mode to systematically establish how two functions compare to each other, when it comes to their orders of growth.
For that, you need to compute the limit Fifty = lim(f(due north)/one thousand(north)) when n → ∞. If such a limit exists, its value tells you right away which asymptotic notations are valid when comparison f(n) with g(n):
- If L=0, then f(n)∈ O(thou(n)) and f(n)∈ o(thousand(northward)).
- If L → ∞, and so f(northward)∈ Ω(thou(due north)) and f(n)∈ ω(1000(due north)).
- For other constant values of Fifty, so f(n)∈ Θ(g(north)).
As an example, consider again f(n)=n³ and m(n)=2n³+northward. For these functions, you will discover that L=1/2, which ways that northward³∈ Θ(2n³+n). (Merely note that, by definition, it also means that n³∈ Ω(2n³+due north) and n³∈ O(2n³+n).)
Final Thoughts
In order to use asymptotic notations like Big O, yous don't really need to have an in-depth understanding of the math behind them. Nevertheless, it may be useful to know what they mean and how they are defined, especially when the relationship between two functions is not so obvious. Is Θ(log(n)) faster than Θ(√n)? Is O(2ⁿ) the same as O(3ⁿ)? What about Ω(log₂(n)) and Ω(ln(n))? At present that y'all know how these notations are mathematically divers, yous can try to find answers to such questions by yourself.
Disclosure: This postal service contains 1 or more links from the Amazon Services LLC Assembly Program. As an chapter, I get commissions for purchases made through those links, at no actress cost to the customer.
Mathematics How to Read Large Theta and Small Theta
Source: https://towardsdatascience.com/the-math-behind-big-o-and-other-asymptotic-notations-64487889f33f